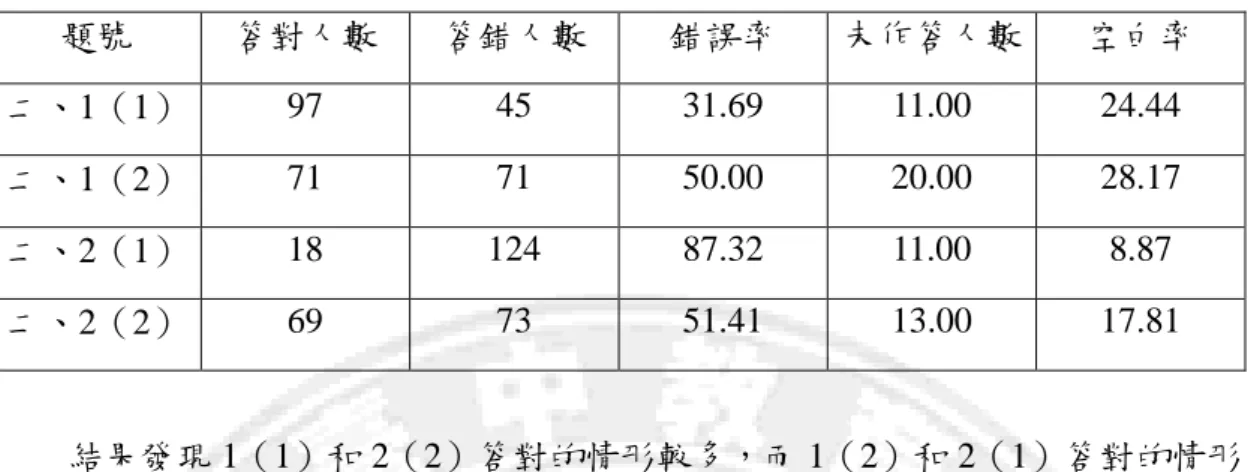
國立臺中教育大學數學教育系碩士班碩士論文
指導教授:胡豐榮 教授
許天維 教授
雲林縣國中生
一元一次方程式錯誤類型之研究
研究生:郭輝煌 撰
中華民國一○三年一月
I
謝 誌
自從任教數學課的第一天開始,就期待著學生都能聽得懂數學概念,並能快 樂地學數學且不放棄數學,就在此念頭下,研究一些相關文獻,且經家人及學校 同事鼓勵之下考進臺中教育大學數學教育學系碩士班,我就期待著寫出能在教學實 務相關的論文來,經三年半的時間研究與施測論文終於完成。 完成時總會想到經過的點點滴滴以及一路上支持的家人及師長,首先要感謝 胡豐榮教授和許天維教授三年半的辛苦指導,接著要謝謝雲林縣淵明國中的前任丁 校長及現任方校長,和數學領域的所有教師同仁,對我在教學與施測上的配合,讓 我三年半的研究所生涯更加充實,更要感謝的是三位口試委員─施淑娟教授老師與 辛俊德教授與鄭裕篤博士細心的審閱,建議與批評,讓這本論文更加豐富完整。 接著要感謝賢內助,本校教育所陳羽暄,對我在學術與學問上的要求,以及生活上 的關心與照顧,您是我心中永遠的貴人,寶貝女兒采蓉,這段特別給你,謝謝你陪我 走過這些日子,謝謝你們,我愛你們。 最後,要感謝南投縣集集國中曹校長與輔導室前任黃主任與現任吳主任與人事室潘 主任,使我研究所論文能順利完成,要感謝幫助我、關心我完成論文的師長與同仁, 謝謝大家。 郭輝煌 謹誌于 國立臺中教育大學數學教育學系 2014.01.13中 文 摘 要
本研究以發展一份具有信度及效度的二階段評量紙筆測驗,對國中生一元一 次方程式的概念進行施測,以探討學生在此單元之解題情形、錯誤類型以及所造 成錯誤的原因。研究以三個階段來了解學生在一元一次方程式中的基本概念,由 開放式問卷以二階段評量紙筆測驗,並透過晤談方式探討分析學生犯錯的原因及 錯誤類型。 研究結果如下: 一、對二階段評量診斷的紙筆測驗發展: (一)信度方面:內部一致性係數均大於刪題後之信度而且判定類型均為 A, 均作保留。 (二)除了以開放式之問卷及晤談方式了解及搜證學生的錯誤類型之外,本研 究的工具還利用雙向細目表來檢驗診斷評量的內容效度,並且經過多次 的施測分析以及探討、來篩選檢驗題目。 二、錯誤類型的發現:以下列九大分類方式來說明: (一)文字符號的意義。 (二)文字符號的列式。 (三)文字符號的簡記(合併)。 (四)求式子的值。 (五)能了解一元一次方程式。 (六)列一元一次方程式。 (七)能了解一元一次方程式的解。 (八)解一元一次方程式(等量公理) (九)應用問題(代數文字題)。 關鍵詞:二階段評量、錯誤類型、一元一次方程式III
Abstract
Evaluation of the second phase of a study to develop with the reliability and validity of written tests for junior high school students one dollar equation Surveying concept to explore students' problem-solving situations of this unit, the error caused by the wrong type, and reasons. Three stages of research to understand the basic concepts of the students in one dollar equation by two-stage open-ended questionnaire to assess written test, analyze and discuss the reasons for students to make mistakes and the wrong type of way through the interview.
Conclusion of the study is divided into two parts to illustrate:
First, two-tier the development of paper-based diagnostic assessment:
(1) Reliability: the internal consistency reliability coefficients were greater than after deletion and determine the type of questions are A, were retained.
(2) In addition to the open-ended questionnaire and interviews and evidence collection methods to understand the types of errors students outside the research tools also used to test the two-way breakdown diagnostic assessment of content validity, and after surveyingrepeatedanalysis anddiscussion,to screentestsubject. Second, the error pattern: nine categories in the following way to illustrate Significance:
(1) The text symbols. (2) Column-text symbols.
(3) Abbreviated text symbols (combined). (4) Find the value of the formula.
(5) Understand one dollar equation. (6) A way to drive out one yuan.
(7) To understand one yuan a solution of the equation. (8) Solving a linear equation (the same amount of axioms). (9) The application of (algebraic word problems).
目 次
第一章 緒 論……… 1
第一節 研究背景與動機 ………1
第二節 研究目的與待答問題 ………3
第三節 名詞釋義 ………3
第四節 研究限制 ………4
第二章 文獻探討 ………5
第一節 一元一次方程式之相關研究 ………5
第二節 一元一次方程式錯誤類型概念之相關研究………12
第三節 錯誤類型及錯誤原因………21
第四節 二階段評量………25
第三章 研究方法………29
第一節 研究設計與對象………29
第二節 研究工具………31
第三節 研究流程………32
第四節 資料分析………35
第四章 研究結果與討論………37
第一節 發展初步二階段評量工具………37
第二節 編製二階段評量………53
第三節 錯誤概念之分析………70
第五章 結論與建議 ………91
第一節 結論………91
第二節 建議………96
參考文獻
………99
一、中文部分………99
V
二、英文部分………102
附錄 ………107
附錄一 開放式問卷………107
附錄二 初步二階段評量工具………109
附錄三 內部一致性係數分析表………114
附錄四 修正後的二階段評量工具………138
附錄五 正式的二階段評量診斷工具………143
表 次
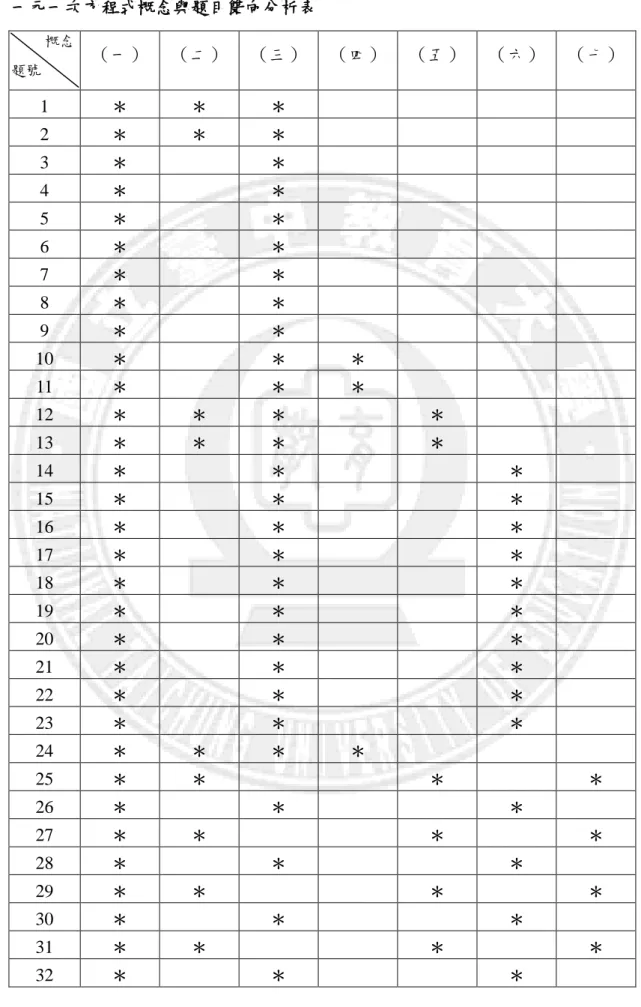
表 3-1 雙向細目表 ………32 表 4-1 開放式試卷錯誤情形分析表 ………37 表 4-2 開放式試卷錯誤分佈情形 ………39 表 4-3 學生錯誤情形分析表 ………40 表 4-4 開放式試題分析情形 ………40 表 4-5 學生在「文字符號的意義」中,作答情形之統計表 ………41 表 4-6 學生在「文字符號的列式」中,作答情形之統計表 ………42 表 4-7 學生在「文字符號的簡記(合併)」中,作答情形之統計表 …………43 表 4-8 學生在「求式子的值」中,作答情形之統計表………44 表 4-9 學生在列一元一次方程式中,作答情形之統計表………45 表 4-10 學生在解一元一次方程式等量公理中,作答情形之統計表………47 表 4-11 學生在應用問題的文字題中,作答情形之統計表………50 表 4-12 鑑別度的評鑑標準………62 表 4-13 一元一次方程式概念與題目雙向分析表………63 表 4-14 題號 1 之學生作答分析表………71 表 4-15 題號 2 之學生作答分析表………73 表 4-16 題號 3 之學生作答分析表………75 表 4-17 題號 4 之學生作答分析表………76 表 4-18 題號 5 之學生作答分析表………77 表 4-19 題號 6 之學生作答分析表………79 表 4-20 題號 7 之學生作答分析表………80 表 4-21 題號 8 之學生作答分析表………82 表 4-22 題號 9 之學生作答分析表………84 表 4-23 題號 10 之學生作答分析表 ………86 表 4-24 題號 11 之學生作答分析表 ………87 表 4-25 題號 12 之學生作答分析表 ………89 表 4-26 題號 13 之學生作答分析表 ………90 表 4-27 題號與概念雙向細目表………93VII
圖 目 次
圖 2-1 摘自〈九章算術〉中的方程組………6 圖 2-2 摘自〈九章算術〉中的一元二次方程式………6 圖 3-1 發展二階段評量工具研究架構圖 ………30 圖 3-2 研究流程圖 ………34 圖 4-1 試題診斷分析圖 ………60第一章 緒論
本章共分為四節,第一節為研究背景與動機、第二節為研究目的與待答問 題、第三節為名詞釋義、第四節為研究限制。第一節 研究背景與動機
近年來隨著《師資培育法》的實施,不少多元背景的教師投入數學科教學行 列,而國中數學科的知識似乎是難不倒每一位數學任教的老師,皆可以洋洋灑灑 在教學的活動中發揮。但經常會聽見,教師們有些難解的想法,為什麼已經教了 許多遍了,相同題型的類題也做了好幾題了,就是不見得學生的進步,而消極的 想法便是學生們本身不用功、不專心。讓數學科的教師深感無奈,也使學生在每 一次的學習遭受到挫敗而失去興趣,更甚者則放棄數學,視學習數學為畏途。林 碧珍(1985)認為數學概念是日常生活中所接觸的概念中最抽象的。所以學生在 抽象概念中要將數學學好,便是一件非常不容易的事。黃台珠(1984)指出教師 最重要的任務是增進學生的概念,加強學生思考的能力以及解決問題的能力。而 概念的學習常在教師演講的教學以及學生聽抄的學習方式下,產生一些錯誤的概 念學習,而教師若在此時未能及時了解學生錯誤概念形成的原因,並進而診斷教 學,便會錯失最好的補教教學時機,學生也因一個概念錯誤而影響到其他概念的 學習。 實施九年一貫以來教育改革的腳步,不僅在編製教科書上開放給各個坊間書 商以求教材之變化,繼有多元教學方法之產生以利學生之學習,連在評量方式上 也相繼出現多元評量的方式,不再像過去傳統的紙筆測驗。也許傳統的紙筆測驗 適用在總結性的評量上,然而在形成性的評量上,便不容易看出學生在學習的過 程中到底是在那一個環節出了錯誤,所以目前有許多的評量雖然仍是以紙筆測為 主,但在方法上漸漸發展能看出學生正確或錯誤的概念內容,如二階段評量、複 式評量、QUASAR、動態評量等。這些評量方式不若過去教師批改考卷的習慣, 過去教師批改考卷多半嚴格要求學生全對才給予分數,尤其是在計算題的批改上 也是相當嚴謹,學生寫錯一個環節便視為不會,而在填充題上也不能看出學生整2 份考卷是那一個概念出錯,只能判斷該題是對與錯,寫對者可以知道學生了解該 題的作法,寫錯者教師也不能從考卷上看出學生那裡不會,即使選擇題選對了正 確的答案,也有可能是猜對的情形,所以成就測驗或是傳統紙筆測就無法了解學 生的錯誤概念為何?因此發展一份有效的診斷式測驗工具,來測試學生的學習概 念,進而了解學生的學習情形,對日後教學也可以提供很大的參考價值,這是一 件很重要的課題。 教師若能了解學生錯誤概念形成的原因所在,在教學上自然可以舉出正反的 例子,來指引學生的學習,所以探討學生錯誤類型和錯誤概念形成的原因,可以 幫助教師在教學上實施有效的診斷教學,避免學生對一個錯誤的概念,一直重覆 系統性的犯錯。而教師研究學生某單元的錯誤概念,是一項非常具有挑戰性且困 難的工作。困難的地方在於過去絕大部份的學生對於數學的發生恐懼,收集資料 時,深怕學生的回答是不知道,另一方面教師們也習慣按照課本教學以及傳統的 紙筆測驗,致使研究無法深入,因此興起想要挑戰的慾望,希望能夠突破傳統的 教學與評量架構。 柳賢(2001)指出二階段診斷評量能診斷出學生的錯誤概念,幫助教師對學 生學習情況能更進一步的深層了解其內涵。所以給了研究者嚐試的勇氣和可靠的 編製工具方法。數學科二階段式的評量工具可以有效的診斷出學生在數學概念上 的正確性,特別是在九年一貫課程實施以後,多樣化的教學措施應該是數學教師 未來努力的方向(柳賢,2001)。 基於上述分析,為避免學生在學習一個概念發生錯誤時,連帶有關的概念也 發生錯誤的情形之下,林碧珍(1985)指出數學概念較抽象具有前後連貫,往往 一個概念是經由某些概念的抽象後再抽象後而形成。所以學生對第一個基本概念 的了解是相當重要的課題,同時也關係到日後學生學習的信心和數學概念的正確 性,並且也可以避免學生發生再犯相同錯誤的情況。本研究將採取二階段評量來 分析國中學生對『一元一次方程式』錯誤類型以及成因,並了解學生的學習困難 所在,提供日後可以讓教師們依據此研究結果設計教學活動單元,檢驗自己的教 學活動是否有助於加深學生正確的數學概念,並提高學生學習數學的興趣、能力 以及學習的成效。
第二節 研究目的與待答問題
本研究係對雲林縣某國中,五個國一班級的學生和五個國二班級的學生進行 二階段診斷評量,希望發展出一份具有信度及效度的一元一次方程式二階段評量 診斷工具,以利日後教師在進行此單元時可以參考此項研究結果,並利用此二階 段診斷評量工具來探討國中學生在學習數學概念過程中產生一些錯誤概念以及 錯誤類型的成因,而將這些錯誤概念歸納並進行補教教學活動,也能依此項研究 結果做為日後教學活動之設計參考,使教師在進行該單元教學時可以參考應用, 針對學生一些錯誤概念加以導正,幫助學生有效學習此單元及提高學生的學習興 趣,所以本研究歸納出有以下的目的: 一、發展出一份具信度及效度的一元一次方程式紙筆測驗試題。 二、藉由二階段診斷評量了解學生學習一元一次方程式錯誤概念形成的 原因。 三、藉由二階段診斷評量工具找出並歸納學生一元一次方程式錯誤概念 類型。 根據上述之研究目的,形成以下的待答問題: 一、探討如何發展一份具信效度的一元一次方程式二階段紙筆測驗試題? 二、分析二階段診斷評量對國中生一元一次方程式的錯誤類型為何? 三、探討二階段診斷評量對國中生一元一次方程式錯誤概念為何?第三節 名詞釋義
一、二階段評量: 本研究評量分成兩種方式,先以開放式的紙筆測驗,再從評量問卷中歸納學 生可能的作法及原因或經由晤談獲得學生的想法,製作二階段評量試卷,其內容 第一階段為判斷對錯,第二階段為選擇理由為何,並依此作為晤談時的樣本選擇 參考。 二、錯誤類型: 本研究將學生從文字代表數出現到文字式子的化簡運算以及解一元一次方4 程式,乃至應用問題等學生所產生的錯誤概念加以分析,並經由晤談的資料分析 得到錯誤類型。 三、一元一次方程式: 等式中只有一個未知數,可以有幾個相同未知數且未知數的次數相同,作同 類項的化簡或移項,而且未知數中最高次數只有一次。
第四節 研究限制
一、本研究採用的樣本為雲林縣某國中,一年級五個班級的學生共 142 人作為本 研究第一階段施測的對象以及二年級五個班級的學生共 151 人作為本研究 第二階段施測的研究對象,因無法擴大研究對象,本研究結果不宜對其他學 生引用或作為其他單元推論,若要作相同的推論時,應加以分析研究對象背 景是否有相似之處,否則不宜作過度的推論及引用。 二、本研究由於研究群時間及人力的限制,研究結論乃由研究者與數學專家討 論,因此研究結論僅少數人的意見,若再能增加討論分析的研究群,其可信 度會佳。第二章 文獻探討
第一節 一元一次方程式之相關研究
學習一元一次方程式之前對於未知數的引用正是代數學習的開始,所以本節 以文字符號的表示、代數解題及方程式之相關概念研究加以歸納整理。 一、文字符號的發展 根據 Kieran(1992)對代數的歷史研究,依西方數學不同時代的發展特徵而 將代數的發展分為三大階段:一為文辭代數階段,二為簡單代數階段,三為符號 代數階段,方吉雄(2001);或說代數符號的生長分為三個時期:第一期為「逐 字期」,第二期為「簡字期」,第三期為「符號式」,王懷權(1992)。(一)文辭代數階段(rhetorical algebra stage)
文辭代數階段指的是在古代希臘數學家丟番圖(Diophantus of Alexandria, 約 公元 250 年)提出運用符號之前,這階段的特徵是使用一般語言敘述一些特殊問 題的解決方法,但缺乏對未知數的符號或特殊記號的使用。 在公元前 1700 年前的埃及人,已把有關代數方程式計算的資料記載草片文 書,如:蘭德草書(Rhind Papyrus),當中全為文字敘述,含有問題列、答案、 解法、驗算等步驟,而沒有說明為何用那些方法。至於中國古代最著名的數學著 作九章算術中的「開方術」及「方程術」,基本上也都是用文字敘述來表達代數。 在這個時期是代數的開始,雖然文字符號的發展尚未成熟,且各個民族所表 示的方式不同,但大部分都是為了解決日常生活的問題,如兌換錢幣、交換商品、 計算長度面積、在商業或農業上的計算都有著相當大的用處,所以代數的重要在 此階段知其重要性與實用性了。 例如:摘自〈九章算術〉中第 8 章方程的第一個問題: 今有 上禾三秉,中禾二秉,下禾一秉,實三十九斗; 上禾二秉,中禾三秉,下禾一秉,實三十四斗; 上禾一秉,中禾二秉,下禾三秉,實二十六斗。 問上、中、下禾一秉各幾何?
6 上禾 中禾 下禾 實 左 中 右 0 元 代表 x2 +270x+18225 當時的解決方法是這樣的:先用算籌排出有關數字,如圖 2-1,然後利用算籌的 操作把左、中、右三條方程式加、減消元就找出答案。 圖 2-1 摘自〈九章算術〉中的方程組
(二)簡單代數階段(syncopated algebra stage)
從古希臘數學家 Diophantus 用文字縮寫來表示未知量至 16 世紀末左右被稱 為簡單代數發展階段。這個名稱並非指那些數學問題簡單,而是說代數學已經發 展至利用符號及較簡單的符號來代替文字,以表達複雜的代數關係。如文藝復興 時期之使用 p 代表「plus」,m 代表「minus 」等,代數的發展才開始脫離文辭 的階段。 而中國在元朝李冶(1192-1279)所著的『測圓海鏡』十二卷(1248)及『益古演 段』三卷(1259),算是那時中國最早有系統地論述「天元術」的著作。「天元」 是指未知數,「立天元為某某」,正是「設 x 為某某」的意思。用「天元術」來計 多項式或方程,常在未知數之一次項旁記一個「元」字,在常數項旁記一個「太」 字。例如 圖 2-2 摘自〈九章算術〉中的一元二次方程式
(三)符號代數階段(symbolic algebra stage)
這個階段大概始於 Vieta(1544~1603)在 16 世紀用字母來替代給定量。它 的特徵除了代數方程的係數以文字符號表示且符號可如數字演算之外,方程式的 任何一端也可以置零。
由上可以看出文字符號和數學有著密不可分的關係及其重要性。符號系統 是,數學中其中之一的品質保證(Rubenstein and Thompson, 2001)。
Collis(1975)則從學生的觀點,將文字符號的概念分類成六種不同的使用層 次: (1)文字符號為可算出的值(letter evaluated),指文字符號代表一個設定的數 值。如:n+5=8 中的 n。 (2)文字符號可忽略而不用(letter ignored),指文字符號雖然出現在題目中, 但在解題過程中可不加以考慮。如:a+b=43,求 a+b+2=?本例中,前後兩式只在 加 2 的不同,a+b 可加以忽略,而直接求出答案為 43+2=45。 (3)文字符號當作禮物(letter as object),即文字符號為某一代表物的簡寫或標 記(label)。如:以 h 代表某一多邊形的一邊,而不是數字(邊長)。
(4)文字符號當作特定的未知數(letter as special unknown),可以直接加以運 算。如:一多邊形有 n 個邊,而且每個邊長為 2,得周長為 2n。
(5)文字符號當作一般化的數字(letter as generalized number),即視文字符號 代表一組數字而非單一數值。如:c+d=10,且 c<d 中,c 代表小於 5 的數。 (6)文字符號當作變數(letter as variable),即文字符號代表一未定的數值,如 比較 n 和 2n 的大小。 二、方程式 解一元一次方程式時所利用的方法大部份是等量公理或移項法則,等量公理 不論是過去的課程標準或是九年一貫的課程綱要都有提到,而移項法則則在九年 一貫開放各書商編寫教材時有大略提到,但一般在教材上都還是以等量公理為 主,然而大部份的學生都習慣用移項法則來解方程式,也許只是背一些口訣的關 係就能運用到解方程式,但仍會有一些狀況會讓學生有所混淆,例如: 6 2 1 x , 學生會搞不清楚這裡的「-」是什麼性質?通會選擇兩種運算,就是負變正,乘
8 2 1 變成除以 2 1 ,而計算錯誤。
Kieran(1989)、Booth(1988)、English and Harford (1995)等學者認為「等 號」是關鍵,是因為部份學生受到先前算術經驗的影響,往往只注意到等號是「do something」 的符號,代表的是「接下來我要做的是」、「答案是」、「結果是」…. 等等解題的過程,而非數學上量關係。Kieran 發現部份學生可能誤解了教師的語 意,例如在解方程式 x +3=8 時,教師告訴學生「移項時要換邊變號」,本來教 師預期的是學生將 3 換邊並且變號(加變成減),而轉化為 x =8-3,但部份學 生誤解教師意思,於是變成了 x =8+3,理由是:「要變號啊!」,根據 Kieran 的解釋,因為學生本來是先將「+3」移至右邊變「-3」,但學生這時記得老師 說過要「變號」,於是把「-3」再變成「+3」。 Küchemann(1981)發現字母在一開始即被賦予數字值,例如在解x +3=11 時,學生利用回憶數字事實 8+3=11 的方式,找出 x=8,而非是對未知數 x 施 予運算以解出 x 值 (引自何基誠,2002)。 三、代數文字 不論是過去的課程標準中的一元一次方程式或九年一貫課課程綱要的一元 一次方程,都會有應用問題的出現,而這也是利用代數來解決學生們最擔心的應 用問題。國小因過去未曾學習過設未知數,所以在解方程式時有些是利用列式看 出一些規則,然後推算出答案,例如: 有 5 元郵票和 12 元郵票兩種,小明總共買了 18 張郵票共花了 160 元,那麼 小明買了 5 元郵票和 12 元郵票各多少張? 國小作法: 5 元張數 1 2 3 4 5 6 7 8 12 元張數 17 16 15 14 13 12 11 10 總 價 209 202 195 188 181 174 167 160 由上表便可以找出 5 元郵票買了 8 張,12 元郵票 10 張。雖然不必用到未知 數便可以解出答案,但似乎需要花一些時間來列表。而另一種不需要列表也不需 要未知數就可以解出答案。假設 18 張全部買 12 元的郵票,那麼需要 216 元,但 實際上只花了 160 元,所以多出來的 56 元便是多買了 12 元的郵票,必須從中扣
除 12 元的郵票,而一張 5 元郵票和 12 元郵票相差 7 元,56 元有 8 個 7,換句話 說要換掉 8 張 12 元郵票,也就是有 8 張 5 元郵票,10 張 12 元郵票,其算式為: 12×18=216 216-160=56 56÷7=8 18-8=10 此種方法,有些同學可以很快就想到,有些同學必須由列表才可以看出端倪甚至 有些同學是無法理解的。如果這一題用國中生的作法,也就是假設未知數列方程 式。國中作法: 設 5 元郵票買 x 張,則 12 元郵票買(18- x )張 依題意列方程式為 5 x +12(18- x )=160 5x +216-12 x =160 -7x +216=160 -7x =-56 x =8 18-8=10 以上述作法可以看出只要假設未知數,再依題目列方程式,解方程式就可以 知道答案,而這樣的解法似乎有些機械化而對於理解重點在於題目,與上述解題 有不同的理解感覺。所以有些同學認為有了未知數對於解方程式有些幫助,可以 免除一些歸納的步驟,而這也就代數的功效了。但是教師們對於應用問題的教學 卻他們感到最難的一個環節,而學生們對於未知數的使用及意義也不了解。 Hammer(1957)的研究中證實在代數文字題解題中,約有 75%的學生無法清楚 了解真正的問題。表示學生在解文字題的時候對於題目中要他們解出什麼,他們 感到疑惑,不知道題目的用意為何,而影響其作答狀況。
Clement, Lochhead and Monk ( 1981)研究指出,學生在將簡單句子轉譯成方 程式時,呈現很大失敗比例。學者認為這樣的現象主要的因素是學生們不能了解 題目的意義,而且透過句子意義的了解,再以代數樣式來表徵,是一般所謂靜態 比較解題思維是導致失敗的關鍵原因。
林碧珍(1990)的研究指出學生解文字題的能力比基本計算能力差,其中低 程度的學生勉強會朗讀題目,但不懂題意,沒有任何解題計劃,缺乏概念性的理
10 解。 林清山、張景媛(1994)提出學生在代數應用題錯誤概念有以下幾點: (一)題意轉譯的錯誤概念 包括學生對於關鍵詞的詞義無法充分了解,學生對於問題中哪些是無用的 條件辨識不清。 (二)問題整合的錯誤概念 包括缺乏基本的數學概念,無法察覺到所計算出來的答案是否會理,學生 不會做假設,學生套用固定的模式而不隨問題的變化而加以改變等。 (三)解題計劃及監控的錯誤概念 未能暸解己知條件與未知條件之間的關係,以致假設與式子不符;無法針 對不同的問題採用不同的解題策略;學生以為一個題目只有一個解法,學生會受 前後題型的影響而採用不當的解題策略。 (四)解題執行的錯誤概念 在解方程式時會產生移項的錯誤,移項的錯誤多半是因為學生缺乏等號兩 邊等值的觀念,學生在使用消去法時容易產扛正負混淆的情形。 Kilpatrick(1967)以 Pólya 想法為依據,探討八年級學生解決文字題時的策 略,發覺受試者使用的解題策略約有:(1)畫圖,(2)使用連續漸進,(3)詢問 解決方法的存在與獨特性,(4)演譯,(5)運用算式,(6)運用嘗試錯誤,(7) 核對結果等。Kilpatrick 發現受試者所使用的策略不多,而將各階段的解題策略 重新修正為(引自陳慧珍,2000): (一)了解問題: 1.辨認未知資料或條件。 2.畫圖。 3.引入符號。 (二)擬定計畫: 1.重新敘述問題。 2.考慮相關問題。 (三)執行計畫: 1.使用連續漸進。 2.發現結果前進檢查步驟。
(四)檢討 1.檢查結果是否合理。 2.檢查結果是否符合條件。 3.回溯論證的步驟。 4.使用其他方法獲得結果。 張景媛(1994)指出一般人認為學生只要了解題目的語意即題目文字的敘述 可以明白,對於簡單的文字應用題學生只要依解題步驟來解題應該是沒有問題 的。但目前教學活動中時常需要使用到各種方式的語言活動,如聽、說、讀、寫 等,而人們外在不同語言表達方式和內在的心理表徵是相互依存,在數學學習方 面,這兩種關係表現在兩方面,一為個人對於內容或公式的了解需依賴其在這方 面的特殊知識,一為經由語言活動,引導個體從不同的角度思考問題,使有助於 問題解決。 由上述文獻綜合探討,研究者認為對於方程式的解題技巧歸納為以下幾點: (一)學生對於冗長的文字敘述,不知道題目要他解決的問題是什麼,甚至 與他所解讀的意思產生衝突,而使學生不知所措,也由此產生失落感 及挫折感。 (二)假設未知數與列方程式的條件,認為有一定的程式規則,不知道條件 是可以互相思考,沒有那一個條件一定是假設未知數哪一個條件是列 方程式的條件。 (三)對於文字代數題的每一個文字敘述,都認為是一種必要的條件,必需 使用到,因此影響到解題的正確性。 (四)學生習慣問什麼便假設什麼,如果題目敘述改變方式問問題,這樣的 文字代數題學生便無法轉彎假設未知數,也就是前面的解題題型概念 干擾到不一樣的解題型式概念。 (五)文字代數題可以利用驗算的工具來檢驗自己算得是否正確。學生解題 後無法依題目的意思重新將所列的方程式解讀一次,檢驗自己當初所 列的方程式是否正確。 關於文字代數題,研究群最後一致認為,大部份的學生都是因為看不懂題目 的關係而影響數學解題的能力,如果想要提昇學生解決應用問題的能力,在語文 能力及閱讀方面便要特別加強,甚至可以讓學生自己去解讀題目的意義,因為一
12 般學生的計算能力都是沒有問題的,只要他能了解題目的涵意,便有能力解題, 如果在最後可以和數學知識連結整合,相信文字代數題便不是什麼問題了,而學 生就可以輕鬆解題了。當然要利用未知數解題就要對未知數的意義了解並且能接 受它和接受數字是一樣的感受。
第二節 一元一次方程式錯誤類型概念之相關研究
本節一樣以文字符號和有關方程式以及文字代數題之相關研究分別作以下 的敘述探討: 一、文字符號(未知數) 文字符號是學生在學習代數前最先接觸到的知識,而它在形式上有別於數字 的計算,學生接受數字的計算合併,但對於一個文字的計算合併或文字和文字的 合併計算,學生便認為不是那麼的自然感覺了。 戴文賓(1999)研究國一學生由算術領域進入代數領域時發現迷思概念為: (一)有關代數式的意義:在代數式求值問題中,學生會把 3 x 當作 3+ x 。 (二)有關同類項的意義與合併規則: 1、只處理含x 的同類項,常數項則不合併處理。 2、不接受含有加號的式子當作答案,如 3x +4,會再將不同類合併處理 變成 7x 或 7。 3、不確定x =1 x ,而會將係數忽略不計,如 3 x + x =3 x 。 (三)含括號的化簡問題: 1、括號外的數字只和括號內的第一項相乘,忽略第二項。 2、括號外的數字如果是負數時沒有變號。 3、不知道括號內的運算是要和括號外那一項作運算。 Küchemann (1978)根據 Collis 對文字符號使用概念層次的分類,以 3000 個 平均 13 至 15 歲的學生為研究對象,並從學生認知能力的不同,來探討學生對文 字符號的瞭解情形及成就表現。其研究結果發現學生成就表現均低,而且屬於具 體運思時期的學生只能處理前三種文字符號的概念(即文字符號為可算出的值、 文字符號可忽略而不用、文字符號當作物體);學生必須發展到形式運思時期,才有能力將文字符號當成特定的未知數、一般化的數字,甚至在到達形式運思後 期之後,才能將文字符號當成變數來處理。由 Küchemann (1981)所主持的 NCTM 研究報告結果顯示,大部分 13 到 15 歲的學生會把文字符號當成具體的實物或具 體實物的標記(label for concrete objects)。
陳盈言(2001)在其研究中發現學生在變數(文字符號)概念上的錯誤有: (一)文字符號與數字混合運算上的錯誤,包括: 1、帶分數模式,如 8+g=8g 2、加法指數模式,如 e+e+e=e3。 3、不同類項擺在一起,2a+5b+a=3a5b。 4、係數與文字符號分開處理,如 2a+5b+a=8ab。 (二)未有符號代表未知數的概念。 (三)未能以符號表示一般化。 (四)不同符號代表不同的迷思。 (五)認為文字符號代表 (六)正數,而忽略了負數。 (七)沒有單元化的概念,學生不能將不同的文字符號組合看作一個整體。 在 Tonnessen(1980)的博士論文中,進行對文字符號作分類,即分成符號、範 圍及元素的自由表徵,去測量美國中西部大學生文字符號概念的發展。發現學生 發展的文字符號概念的層次很低。因為他的研究並未注意到學生使用文字符號的 情形,只能知道學生是否瞭解這些概念的意義。所以這個研究無法證明學生發展 到達文字符號的某一層次,就可做為預測學生使用文字符號到那一層次的指標, 即有能力去說明文字符號的意義並不保證有能力去使用它。因此,未來的研究方 向有必要朝向文字符號使用情形的瞭解。 Booth(1986)研究指出學生先前的算術經驗影響其對未知數學習。如有些 學生將 2+x 化簡為 2x 是受到算術中 2+ 2 1 = 2 1 2 或 42 代表 4 個 10 加 2 個 1 等 等類似經驗影響。另外 Booth 也觀察到有些學生認為 xyz-yz 可以寫成 x。 Wagner(1981)研究改變方程式及函數中的文字符號名稱,對學生的影響情 形,即欲了解學生是否知道改變文字符號的名稱並不影響方程式及函數的意義。 他發現許多學生固著於所命名文字符號刻板性用法,並不能隨著文字符號名稱的
14 改變,而做適應性的解題,甚至有些學生認為替換不同的文字符號,便改變了整 個題意,而必須用完全不同的方法去做答。由此可知,有些學生並不瞭解文字符 號所代表的意義。 Rosnick(1981)指出學生在數學中文字符號的使用方面,有一些共同的錯誤。 他發現學生會混淆代表實物的文字符號和代表實物數值的文字符號概念。 1982 年國家教育進步評量(National Assessment of Educational Progress)的研 究結果亦顯示學生對文字符號概念的低成就現象(Carpenter, Kepner Jr., Corbitt, Lindquist, & Reys, 1982)。Carpenter et al.以 13 至 17 歲的學生為研究對象,並根 據學生的表現去歸納其代數技能及其瞭解情形。他們發現 91%的學生能利用”□” 的概念去解一些簡單的方程式問題,如:4×□=24,卻只有 65%的學生能解使用 文字符號的方程式問題,如:6m=36。將題目的運算數字變大,其正確的反應則 降至 30%,只有 58%的 17 歲學生能正確的以 t+9 把”比 t 大 9 的數”表示出來, 其他類似的問題也只有 43%做出正確的反應。由此可知,學生在解方程式及利用 文字符號列出方程式方面,存在著學習的困難。
Clement, Narode and Rosnick (1981)從 15 位學生的面談過程中,也發現了這 種共同的錯誤。因此,『每 17 個人(P)中,便有 3 輛汽車(C)』的問題,學生便會 犯『3C=17P』的錯誤。 郭汾派(1988)參考英國 CSMS 小組所設計的題目對全國分區抽樣測試國中生 在文字符號概念的主要錯誤類型,發現其常見的錯誤有: (一)帶分數模式 2 1 7 2 1 7 之影響,而有 8+g=8g 之迷思。 (二)係數、文字分別處理。如 2a+5b=7ab,4×(n+5)=4n+20=24n。 (三)不同類項擺在一起。如 h+h+h+h+t=4ht。 (四)不知如何使用符號。如 5×(e+2)=5e+2 或 5×e+2。 (五)忽略數據資料。如設 c+d=10 且 c<d,求 c 時,答案多為 c=10-d,而 忽略 c<d 之條件。 (六)認為不同文字代表不同數。如 K+M+N=K+P+N 之題目要回答 M=P 之答案感到困難,認為不同文字沒有相等之可能性存在。 (七)將文字當作特定數處理:學生易認為答案一定是一個已知數的錯誤觀 念,尚未能建立好公式一般化的觀念。
(八)受定義影響。學生有時會誤解題意或不明白題意,以致作出錯誤的答 案。 (九)重新設定未知數。習慣以 x ,y,z表示未知數,換成 a,b,c 或其他 符號,其認知就會不同,也尚未能體會文字符號只是“符號”,不 管以什麼來代替都可以的地步。 (十)不能辨別符號與物品。如對甲牌鉛筆每枝 7 元,那甲支甲牌鉛筆是 7 甲元感到困難。 (十一)文字符號當有次序的特定數。學生隱約會把 a,b,c…當成 1,2, 3 之順序來處理,如若甲+2=丙,那麼會把甲+4 回答為『戊』。 (十二)文字符號只當不為負數的數字處理。如設 c+d=10,且 c<d,求 c=? 很高比例的學生會回答為 1,2,3,4 或 0,1,2,3,4。 郭汾派和林光賢(1989)以臺灣地區的國中學生為研究對象,建立了國中學生 文字符號概念的發展層次。他們發現 50%左右的國中二、三年級的學生,只會 做單一文字符號運算、處理文字符號只當特定數或只有數字計算等結構簡單的題 目。 綜合上述文獻探討,發現學生對於文字符號運算,並不容易接受: (一)如 2+2+2+2+2+2=2×6,依照九九乘法表的意思可知是 6 個相加, 但若把 2 換成x ,似乎對 x + x + x + x + x =?心中便有許多的疑惑。 (二)一些簡單的運算當遇上了未知數時,也變得不知道要如何運算了。如 4× (5+6)=?學生可以計算括號內的值再乘以 4,但 4×(x +6)=?此 時無法算出括號內之值,即使教了分配律或去括號法則,學生也往往只乘 到第一個數,第二個數卻忘了。 (三)若是碰上兩個以上的未知數學生對於運算的部分更加分辨不清了。 (四)未知數習慣用 x ,對 x 的運算也許熟悉,若換了未知數之使用,也許又必 須要重新適應了。 (五)若是 x 是個未知數或甲是個未知數時,其它物品的名稱最好不要與未知數 有相同的名稱了,否則學生更搞不清楚了。 二、方程式(等號) 學生解方程式時,可能會遇到對文字符號化簡合併,及利用到等量公理解程
16
式。對於方程式中的等號,一般學生對於等號的意義只是計算的結果,並沒有兩 邊對等的觀念。
Kieran(1992)的教學研究顯示多數學生把等號的右邊當成運算的結果,他們 對等號的說明,所舉的例子為左邊是一個單一運算而右邊是結果。
Behr, Erlwanger and Nichols (1976) 也指出學生在初學方程式之時,因為受 到過去學習經驗,而認為方程等號右邊是表示運算的答案,所以等號對他們而言 只是一種作出結果的符號而己。 Vergnaud(1984)也強調等價的概念,他認為學習代數的重點是必須能將等號 看成對與等價的概念。同時也指出國小 6 年級學生大都直接以情境中的數值關係 直接運算,而將整個算式寫成一列,如 2.30+3.20=5.50-1.50=4。他們忽略了等號 的對稱與等價性。 Kieran(1989)就非常強調等號的等價概念對解方程式的重要性,因為等價觀 念是學生學習代數的基礎、等價觀念是表徵方程式及解方程式的基礎,具備等價 觀念能對方程式有結構性的觀念。
Benander and Clement(1985)在算術與代數基本課程教學時,以教室觀察、檢 討、面談三種方式,發現學生在「解方程式」時存在下列的錯誤類型: 1. 未知數係數是 1 的察覺失敗:學生認為 a 和 1a 不相等,故無法察覺 a+3a= 1a+3a=4a 算式成立。 2. x = x 的迷惑( x = x confusion):當學生化約方程式得到 x = x 時,可能做下了 x =1 或 x =0 的結論。 3. 無法察覺同類項:學生在判斷方程式中是否有合併的相同項發生了困難,於 是認為 2+ x 可以合併為 2 x ,而不知 2 和 x 是不同類之項次,不可以任意合 併。 4. 切換逆預算失敗:當化簡方程式時,需要用除法時學生卻用減法,而需要用 減法時,學生卻用除法。當學生在解 2 x =5 時,他以 x =5-2=3 的方式解 出 x =3。 綜觀上述,學生在學習解方程式之初應能確定等號的意義,才能利用它來 解決日常生活的問題,並且真正了解方程式的意義,它不只是運算的結果而已, 而是兩邊對等的概念,如此在利用等量公理解方程式之時,才能正確使用並了解 等量公理的涵意。一般學生在解方程式時,通常會有以下幾個步驟:(1)有括號
去括號,(2)利用等量加減法公理將未知數放在等號的同一邊,等號另一邊放數 字,(3)合併同類項,(4)再利用等量乘除法公理解出未知數。但 Herscovics and Linchevski (1994) 認為教師教學時若過份強調此四個步驟的技巧,而忽略了利用 問題解決的技巧解題,學生過度反覆練習這四個步驟,在解題中便容易缺乏評估 過程的能力了。如 2 1 ( 2 1 ( 2 1 x +3)+3)+3=18,若使用上述的步驟來解題,恐 怕對解題時會有些複雜,所以對於解方程式的步驟應要能善加利用而不是一成不 變,這樣才能達到解方程式的目的。 謝孟珊(2000)在以不同符號表徵未知數對國二學生解方程式表現之探討中 指出影響方程式的解題因素分為七大類: (一)運算符號的性質。 (二)運算符號的個數。 (三)運算符號及未知數的位置。 (四)未知數出現的次數。 (五)答案是否為整數。 (六)係數的大小。 (七)題目中是否有括號。 王如敏(2004)歸納統整出影響國中生正確使用方程式的三大主要因素,包 括: (一)對方程式的了解,此包含對未知數的了解,即對文字符號的正確認。 (二)正確的運算過程,大部份學生的問題是由此產生,其包括加減乘除運算、 括號的去除。 (三)具有足夠之先備知識,如答案是否為整數會影響學生是否能正確解題,因 而學生之前對分數概念的了解亦是影響正確解題的關鍵。 綜合上述文獻探討,學生對於解方程式常常會受到下列因素的影響: (一)對於等號並沒有等價的觀念,以為左邊是式子的運算,右邊是計算的結果。 (二)未知數的運算符號性質正或負、位置在左邊或右邊、出現的次數,還有係 數的大小和所解出來的答案是否為整數。 (三)過度強調解題的步驟,未能了解題意使用技巧能力而使得解方程式的過程 趨於複雜化。
18 (四)等量公理死記要訣,正變負、負變正、乘變除、除變正卻搞不清楚運算符 號還是性質符號。 所以在解方程式之時,教師應能引導學生善用等量公理或是解題步驟中的 技巧要能視題目的變化而變化,非一成不變的解題,這樣才能達到解方程式的效 果,讓學生感覺在解決問題而不是製造另一個問題的產生。 三、文字代數題(應用題) 應用問題大概是學生最頭痛的題目,因為其題目長又要了解題目的意義才有 能力解題,而它也是教師在教學單元中比較無奈的一個單元,往往感嘆學生礙於 語文能力解讀的關係而非數學能力不足以致無法解題。茲將有關文字代數題之相 關研究分述如下: Grady(1978)研究探討學生的認知層次和數學解題表現之間的關係。雖然在 他的研究當中,形式運思期的學生和具體運思期的學生在數學解題的表現上,並 未出現顯著的差異。但他發現,形式運思期的學生比具體運思期的學生使用更多 的方法:手段捷思法(means-end heuristic)去解問題。而他進一步地利用回歸分析 的方法,發現除了智商因素之外,認知層次這一因素比其他因素更能說明學生解 題表現的差異。 Niaz (1989)的研究發現,缺乏形式運思理解能力的學生在轉譯代數文字題成 為代數方程式方面,出現了較多的學習困難。 Mayer (1985)代數文字相關的研究指出,轉譯代數文字題的歷程對學生來講 可能是十分困難的,特別是包含關係語句的代數文字題。
Loftus and Suppes (1972)在方析影響問題困難度的因素時,發現學生感到特 別困難的問題是包含有相關性的敘述句,例如:"瑪麗兩年前的年齡是貝蒂年齡 的兩倍,如果瑪麗現在 40 歲,問貝蒂現在幾歲?"
Clement, Lochhead and Monk (1981)研究指出,即使是大學生,在轉譯簡單句 子成方程式方面,也出現很大的失敗比例。像"某大學中的學生人數是教授人數 的 6 倍"的轉譯問題,主修科學的學生所出現的錯誤率是 37%,非主修科學的學 生所出現的錯誤比率則提高至 57%。他們同時也發現,產生這種錯誤的原因有二:
1.不了解題目的意義,只是根據句子中文字出現的順序把文字符號加以順序 的表示出來,即所謂的字序的配對(word order match).
2.由句子意義的了解,再使用代數的圖形表徵,即所謂的靜態比較 (static
comparison)。
Travis(1981)曾以 Paign & Simon 的轉譯原則為架構進行學生解代數文字題的 錯誤分析。這些轉譯的原則包括命令式的替換(mandatory substitution)-如 2 倍代 表乘以 2、功能標籤(function tags)-指依文字的文法功能來轉譯,確認形式上及關 係上的變數名稱、使用輔助表徵及線索。從學生錯誤情形的分析,他認為教師應 鼓勵學生在列式之前,將每一未知量及相關的元素用文字符號清楚的表示出來, 而且教師應多鼓勵學生使用輔助表徵及線索,如畫圖、畫流程圖等。 Mayer(1982)要求大學生閱讀並求解八類代數文字題。例如,有一個問題 為:"一幅長方形的圖畫,其面積比加 2 吋寬的畫框時少 64 平方吋。設這幅圖畫 的長比寬多 4 吋,問此畫的面積是多少?"。這些問題包括了三種陳述句:(1)指 定句:指定某一變數一個數值,如"畫框為 2 吋寬";(2)關係句:表示兩個變數間 的數量關係,如"長比寬多 4 吋";(3)疑問句:求未知數的數值,如"問圖畫的面 積是多少?"。他將學生解題時所犯的錯誤分為遺漏的錯誤(omission error)- 如某 一句話未使用、細目的錯誤(specification error)-如"畫框有 2 吋寬"誤以為畫框有 2 吋長"、轉換的錯誤(conversion error)-如"圖畫的長比寬多 4 吋"誤以為"圖畫長是 4 吋"。 Rosnick(1982a)利用面談方式進行大學生解代數文字題的原案分析,他發現 學生在使用文字符號解代數文字題時,會有定義不精確(imprecise)、不一致 (inconsistent)、似是而非(paradoxical)及過度連結的現象(over-associative),而學生 所出現的這些現象,使得學生視文字符號為無法區別的整體 (undifferentiated conglomerates)。 數學家 Pólya (1945)在怎樣解題一書中,將解題分成四階段:即了解問題、 擬訂計畫、執行計畫、回顧解答。其步驟如下: 1. 小心閱讀問題,了解問題的內容及要求。 2. 儘可能畫圖來幫助題意的了解。 3. 將問題的相關元素以符號或數字表示出來。 4. 用方程式把問題表徵出來。 5. 解方程式。 6. 檢查答案是否符合題意。
20
只是,學校的老師常直覺地以為學生有足夠的能力去將問題加以轉譯,而且 認為只要照著文字的意思,配合解題的步驟便可輕易地求出解答。可是在實際教 學中其結果往往是另人失望的。而且有些研究者也發現,有些學生雖然在代數方 程式方面是成功的解題者,但在解代數文字題方面也和其他同學一樣有著相當的 困難(Berger and Wilde, 1984; Travis, 1981)。
不過即使年代久遠,有經驗的數學老師仍然覺得文字問題是數學中最難的一 個主題,而學生也深感文字問題是最令他們感到挫折的數學內容。 Mayer(1985)研究指出,轉譯代數文字題的歷程對學生來講可能是十分困 難的,特別是包含關係語句的代數文字題。 Wollman (1983)對 Clement 等的研究工作做進一步的研究,他發現造成這些 轉譯錯誤的原因有下列幾點: 1. 做得太快。 2. 列完方程式沒有立即檢驗。 3. 未根據問題的意思列式。 4. 未使用文字符號來列式。 這個研究同時也發現,學生在匆忙解題之際,也能做出正確的檢驗,只要花 十分鐘的時間,要求學生從句子意義了解列式並檢驗方程式,學生幾乎可以達到 100%的成功率。 數學研究者注意到下列問題,張景媛(1989): 1. 數學和數學教學中所使用的語言特色是什麼? 2. 學生在讀寫數學時,會遭遇到哪些是由於數學語言的特質所產生的問題(特別 是從第一種形式的語言轉換到另一種形式時)? 3. 語言理解在問題解決時扮演何種角色?也就是說,問題的陳述如何影響學生 的解題? 4. 語言溝通在數學學習上扮演何種角色? 5. 如何教才能直接教導學生發展數學閱讀能力或理解能力? Muth(1991)的研究指出:學生對於數學文字題的解題能力會因文字題中無關 訊息的干擾而無法解決問題。學生們的觀念中都認為文字題中的所有訊息都應被 使用,因而造成學生問題整合上的困難。 Simon(1980)在其研究中發現學生缺乏用文字去表示未知的量的能力,顯示
缺乏了解代數如何結合數學的關係去解得一個特殊的解之概念。而且當題目取材 自真實情境中時,他們似乎不能就真實世界的狀況來思考,而只把它當作一種按 題目機械式的轉譯文字對應到代數符號的步驟而已。
第三節 錯誤類型及錯誤原因
教師在教學過程若能即早發現學生的錯誤概念及錯誤原因為何,在此階段教 師能多了解學生的想法,能夠思考學生的為什麼這樣做,接著適時地指正學生的 想法,這對學生的學習才能有意義,教學才有成效。一般教師遇到學生對相同問 題,一而再,再而三地犯錯,都會歸納到學生上課不專心,不用心的緣故,再者 對於教師特別提出來易犯錯的地方,學生總是還是做錯,教師總覺得愈提醒愈容 易犯錯,關於以上兩方面的錯誤對於老師來說是相當無奈的,是故教師便以不斷 反覆地練習來加強學生正確的概念,其實效果在老師衡量之下也是不大,那是因 為不找出學生錯誤觀念發生在那一個環節,學生便在此環節繞不出來,練習做得 再多,對他而言是機械式地練習,等題目一有變化他還是不懂。所以教師應能去 尋找學生錯誤的原因在那有那些錯誤的類型並在教學上引導學生正確的觀念,才 能有效幫助學生建立正確的數學知識。 林清山、張景媛(1994)研究表示,學生在代數應用題的學習上會有系統的錯 誤產生,學生會受整個文字題的複雜度、題目中未知數數量的多寡、及題目中負 號及式子組合的影響,而對數學文字題產生錯誤概念。另外,張景媛(1994)又提出 認為國中生對數學文字題的錯誤概念可分成四部分討論:一是語言知識的部分、 二是基模知識的部分、三是策略知識的部分、四是程序性知識的部分。 一、語言知識的錯誤概念分析 1. 學生面對較長的數學文字題時,常不知問題所在,所以會立即放棄思考 機會。 2. 學生看完數學文字題時,只記得解出一個答案,而忽略問題需要兩個答 案。 二、基模知識的錯誤概念分析 有些學生的思考模式和基模知識,有功能固著的現象,因而造成他們再解 答數學文字題時,不管問題的性質,都固定套用他們習慣使用的基模知識。22 三、策略知識的錯誤概念分析 1. 學生未能瞭解已知條件和未知條件的關係,因而在做假設及列出式子 時,未能切題列出正確的方程式。 2. 學生做假設時通常是問什麼就假設什麼,不考慮是否有其他簡易的方法。 3. 學生做假設是一回事,列式子又是一回事,兩者無法連貫。 4. 學生沒有等號兩邊相等的概念,所以列出來的式子並未兩邊相等。 四、程序性知識的錯誤概念分析 在解代數方程式時,最常出現的問題是移項時產生錯誤。 Marshall(1987)將學生的解題錯誤分為六大類:
(一)處理語言訊息的錯誤 (errors in processing language information)。
(二)解釋空間訊息的錯誤 (errors in interpreting spatial information)。
(三)選擇適當步驟的錯誤 (errors in selecting appropriate procedures)。
(四)概念連接的錯誤 (errors in making concept association)。
(五)應用不相干的規則或訊息 (errors in using irrelevant rules or information)。
(六)不專心 (unconcentration)。 Mayer(1985)將學生解題錯誤分成三大類: (一)遺漏的錯誤 (omission error):是對命題不能完整回憶的結果。 (二)細節的錯誤 (specification error):在陳述句中一個變數轉換到另一個變數的 能力不足所致。 (三)轉換的錯誤 (conversion error):無法將關係句的形式轉換為陳述句的形式。 三種錯誤中,以轉換的錯誤最為嚴重,其原因是很多學生對關係的回憶,缺 乏表徵關係的語言知識所導致。 Engelhardt(1982)將學生的錯誤分成四種基本類型: (一)機械性的錯誤。 (二)粗心的錯誤。 (三)計算上的錯誤。 (四)演算過程的錯誤。 秦麗花(1995)將解題錯誤分為四個層次: (一)缺少檢驗工作忽略答案合理性:沒寫答案、沒寫單位、單位寫錯、不知答案 為何、省略步驟、抄寫錯誤。
(二)執行計劃失誤,運算不熟練:基本運算不熟練、不懂借位運算、二種運算混 淆、顧此失彼。 (三)基本概念不清,盲目運算:缺少相關概念知識、不懂數學語言、迷失於關鍵 字中、加所有的數字、無法辨別數據大小、無法辨別數據間的意義、只停留+、 -運算而缺少×與÷概念。 (四)沒有解題能立及作答動機:不會閱讀、一知半解、畏懼作答。 張景媛(1994)提出:過去有關教與學的研究中,教師通常認為學生答錯是 因不小心或誤解題意。呂溪木(1983)的研究指出:學生錯誤概念的產生可能是來 自學生日常生活經驗中所學得的,也有些是來自於學生對老師機械式教學的一知 半解。 綜合上述可以看出學生的錯誤概念來自於兩方面: (一)教師的教學:以講述式的教法,教師以一對三十左右的學生,教師一成不變 的教學方式,為了讓學生多做練習及在趕進度的情況下,反應較慢的學生最後以 自己的生活中的經驗解讀而產生錯誤概念。 (二)學生的練習:學生於課餘時間的練習不足,無法建立自己的思考模式,多半 在練習有著不求甚解的態度,以為自己了解了,題目沒有耐心看仔細,做完題目 又不能細心檢查,而造成錯誤的概念。 Carpenter et al.(1989)研究提出:運用學生思考的知識來教學,會增進學生的 解題策略,而教師也越來越能瞭解學生學習上的困難及學生個別差異的情形。這 對教師和學生而言都有很大的幫助。 謝孟珊(2000)將學生解方程式的錯誤類型分成五類,分別是文字符號認知 錯誤類型、等號的認知錯誤類型、代數式認知錯誤類型、解題策略錯誤類型、解 題程序認知錯誤類型。每一種類型中,舉出學生因表徵不同所造成的解題錯誤: 一、文字符號認知錯誤類型 1. 認為□前面不能有負號。 2. 認為□不能移項。 3. 無法了解□跟□可以運算。 4. 認為不能將□與數字運算。 二、等號的認知錯誤類型 1. 只出現在表徵的錯誤:認為□表徵沒有省略乘號之代數文法;無法將一個
24 代數式看成一個整數;無法正確判斷括號在代數式中的運算結構。 2. 只出現在×表徵中的錯誤:未依照運算結構使用代數文法;不能將分數代 數式看成運算的意義。 三、代數式認知錯誤類型 1. 等號右邊不能接代數式,因為等號右邊是要算出一個數,所以返回去算 一次便要完成,如 x ×2+5=35 其作答為 x =35-5÷2=15 2. 等號右邊是答案。即等號左邊是放待求的未知數符號,右邊是放待求的 答案,所以當未知數的係數是負數時,學生求解便出問題,如 7-□=- 15,□=-15+7,□=-8。 四、解題策略錯誤類型 1. 只出現在表徵中的錯誤…列舉評估法的誤用。 2. 只出現在×表徵中的錯誤…移項法則的誤用。 五、解題程序認知錯誤類型 1. 合併同類項的錯誤。 2. 去括號的錯誤。 Ginsburg(1989)、Harding(1986)認為當學生不瞭解教師所教授的知識和書本 的說明時,往往因為缺少完整的概念或不當的使用數學規則,因而造成錯誤。 黃敏晃(1993)目前我國的小學數學教學法,只要求學生在考試前記住許多 要考的數學知識,而沒有要求他們理解這些知識的行成原由。 Ashlock(1992)認為學生系統性錯誤發生的原因,是在於團體教學中學生並未 具備需要學習之概念與程序之先前理解和技能所致。例如當學生需要具體事例 時,卻被迫記憶一系列複雜機械的行動。於是學生會以最簡單的程序加以記憶, 尤其是學生常常以錯誤程序處理時,卻因正確而得到增強。 由以上的錯誤原因及錯誤類型,可以推論教學的目標是相當地重要,而目前 教育制度似乎還是考試領導教學,教學為了讓學生考出好成績,都會在考前要學 生背好許多考試的數學知識,並不去理會學生是否了解,只檢驗學生公式是否背 熟了會不會代公式,並不在乎學生對公式的由來是否明白,以急就章的方式要求 學生應付考試。而學生在這樣的教學環境之下也習慣了考試的方式,也以最少的 理解方式以及許多練習強迫記憶一些數學知識以準備考試,學生只求會不會做,
答案正不正確,對於訂正的工作不在乎,為什麼會答錯也無所謂,由此學生常常 以錯誤的態度解決,也導致錯誤的概念。所以對於學生錯誤的原因及常犯的錯教 師有必要知道,才能對症下藥。
第四節 二階段評量
要找出學生的錯誤概念,以過去的傳統紙筆測驗是看不出學生在那一個地方 出錯,只知道學生這題做對了,做錯了。選擇題的測驗形式用在評量學生的科學 知識已經行之有年,但是在學生填答的背後,究竟是抱持著什麼樣子的理由,卻 是選擇題測驗形式無法診斷出的 Odom and Barrow(1995)。而以晤談的方式是最 直接找出學生錯誤概念為何,而且是最清楚的方法,但所費時間太多不符經濟效 益。所以,最近 Treagust and Haslam (1986; 1987), Odom and Barrow (1995), Rollnick and Mahooana (1999)建議使用另一種測驗的形式,來診斷學生的科學概 念,此種診斷的工具即為兩階段式(Two-tier)評量診斷工具。柳賢(2000)針對高 一學生進行開放式兩階段評量測驗後提出,經由這種開放式兩階段的評量方式, 教師可瞭解學生是否真正理解所學的知識而非一知半解。一般學科的評量方式多 半採用紙筆測驗,分為開放式與封閉式兩種方式,封閉式測驗較有固定且客觀的 評分標準,而開放式測驗的評分則較主觀,不同評分者,結果可能不一樣,郭生 玉(1985)。 利用二階段評量診斷學生錯誤概念概念的相關文獻有: 陳世峰(2001)發展國小學童聲音概念之 two-tier 評量診斷工具。 陳建蒼(2001)利用二階段診斷評量診斷高一學生在對數函數的錯誤概念後 行個別化補救教學,發現有效減少學生錯誤概念的產生。 唐健文(2001)利用二段式診斷工具研究中學生電磁流及感應電流迷思概念。 陳俊廷(2002)利用二階段診斷評量診斷高中生空間向量學習困難。 林楷植(2002)發展二段式紙筆測驗探討國中生學生力與運動之迷思概念。 李浩然(2003)利用二階段診斷評量分析國一學生分數乘除法運算錯誤概念 類型。 黃琬真(2003)以二段式診斷工具探討國小學童昆蟲概念及其迷思概念之研 究。26 林樹榮(2003)利用兩段式診斷測驗探討國中學生有關元素、化合物之概念。 陳忠雄(2003)利用二階段診斷評量分析高中學生三角函數概念學習錯誤概 念類型。 賴潔芳(2004)利用二階段評量應用在高中生三角函數學習成效之研究 以上研究均指出二階段診斷評量較一般的紙筆測驗更能診斷出錯誤概念,不 論是科學概念或是數學概念,二階段評量均具有診斷概念的功能所以最近都建議 教師採用,由此可知利用二階段診斷評量做為數學科之學習診斷工具已成為趨 勢,而且在幾年當中一直廣泛地被使用。盧秀琴(2003a)指出科學教育評量研 究重心逐漸由重視學生的學業成就,轉而重視學生障礙的診斷;然而診斷式評量 通常藉由晤談來進行,較難以大規模施測,故研究群擬採用「二階層診斷式紙筆 評量」,適合大規模施測調查。
唐健文(2002)二段式診斷工具(two-tier diagnostic instrument)又稱為「二 段式問卷」、「二段式選擇題問卷」等,不同於選擇題的方式,二段式選擇題的每 一題都分為二個部分,學生在作答第一個部分(單一選擇題)之後,還要就第二 部分(也是單一選擇題)回答其依據的理由,第二部分的選項中最後應有一「其 他」選項以備學生有其他想法時寫出其想法。第一個部分的每一個選項在第二個 部分都有一個或一個以上的選項與其對應。當學生在第一個選項正確作答時,還 要看他第二部分的作答是否對應正確。因此,二段式選擇題比起選擇題的方式應 該更能診斷出學生的概念,並且能夠進行對大量學生的施測。Treagust and Haslam (1986;1987)曾利用二段式選擇題的方式來診斷中學生關於植物光合作用及呼吸 作用的迷思概念,研究中認為比起選擇題,二段式選擇題的方式可以得到較佳的 成果。 Franklin(1992)曾發展二段式選擇題的方式來診斷學生在力、光、電、熱這些 方面的迷思概念。許健將(2000)曾利用二段式選擇題的方式來探查高三學生關 於共價鍵及分子結構之迷思概念;唐健文(2001)也曾利用二段式選擇題的方式 來探查中學生關於電流磁效應及感應電流的迷思概念。 本研究乃根據 Treagust(1988)提出的二階段式診斷測驗工具發展的步驟來設 計本研究中的一元一次方程式概念之二階段式診斷測驗工具。茲將其發展步驟簡 述於下:
第一步驟:定義內容 (一) 對於命題知識的敘述之辨識 (二) 發展概念圖 (三) 把命題敘述與概念圖關聯起來 (四) 建立內容的效度 第二步驟:收集學童的迷思概念 (五) 收集有關的文獻 (六) 對兒童進行無結構的晤談 (七) 發展能自由反應的選擇題 第三步驟:發展診斷測驗 (八) 發展二階段的診斷測驗 (九) 設計檢查表 (十) 持續精煉 二階段評量診斷工具顯露出很多信效度的問題。大多數的文獻對於二階段評 量診斷工具之效度皆是採用內容效度或是專家效度。而對於二階段評量診斷工具 之信度都沒有多加的著墨。而信度的增加有助於效度的增加(郭玉生,1998)。 本研究所設計的二階段評量診斷工具分為三個步驟: 第一步驟: 利用開放式問卷收集學生的想法、概念、常犯的錯誤以及因錯誤概念所形成 的答案,作為第二步驟編製初步二階段評量工具之選項答案。 第二步驟: 將收集來的學生概念、常犯錯誤以及因錯誤概念所造成的錯誤答案,編列為 第一段選項之答案,第二段則開放學生寫出理由,第三步驟:修正二階段評量工 具中理由之選項收集。 如:化簡下列各式 ( ) x 5 2 + x 2 1 =
28 x 5 1 x 10 9 x 7 3 x 10 7 其他答案 理由: 第三步驟: 診斷試題將以二階段評量形式呈現,第一段為是否之選項,第二段則理由選 項,主要理由來自第一步驟和第二步驟所收集到學生的概念及想法。如: (5 x + 4) – (3 x + 7)是否為一元一次方程式? □是 □否 理由是( ): 因為(5 x + 4) – (3 x + 7)化簡後 x 的係數為 2,x 項仍存在, 即仍有未知數項。 因為 x 項的次數為 1。 因為(5 x + 4) – (3 x + 7)化簡後 x 的係數為 2,超過了一次。 沒有了等號,一定不是方程式。 其他答案 本研究設計二階段評量工具是依據時間實施程序分為三個步驟來實施及收 集學生學習一元一次方程式的概念,並歸納其錯誤類型。而二階段評量試題則分 成二段選項來診斷學生的概念。
第三章 研究方法
本研究主要的目的在以二階段評量診斷國中生對一元一次方程式錯誤類型 之探討。希望能藉由此次的研究結果歸納出學生在學習一元一次方程式時所產生 的錯誤概念,提供教師在教學上的參考,注意學生易犯錯的概念,即時改正學生 的錯誤概念,以達教學的效果。本章將以第一節研究設計與對象、第二節研究工 具、第三節研究流程、第四節資料處理分述如下。第一節 研究設計與對象
一、研究設計 本研究的目的是發展出一套具有信度及效度的一元一次方程式二階段評量 診斷工具,以診斷學生對一元一次方程式所產生的錯誤概念。所以一方面搜集學 生對一元一次方程式的概念,另一方面修正二階段評量診斷工具的內容。 本研究將採三個步驟作為研究的程序: 第一步驟:發展二階段診斷評量工具為主,首先先以文獻探討有關一元一次 方程式的概念對學生進行晤啖以編製開放式紙筆測驗,以一年級五個班的學生為 進行施測對象,施測完畢後並進行半結構式晤談蒐集一元一方程式概念,分析資 料,初步完成二階段診斷評量工具。 第二步驟:再進行第二次施測,研究對象為二年級之五個班級的學生,蒐集 新資料及分析資料,修改二階段診斷評量工具,並實施前後測以 TESTER for Windows 程式版 2.0 檢驗內部一致性信度,效度方面採取專家效度,邀請專家建 立專家效度,最後完成二階段診斷評量工具。 第三步驟:利用二階段診斷評量工具對二年級的學生進行測驗,然後診斷試 題項目歸類,將學生作答的概念歸類並進行晤談分析,晤談方式以開放式晤談及 半結構方式晤談,內容包括有關一元一次方程之文字符號、方程式、文字代數題 之基本觀念、概念理解、問題解決等項目,利用雙向細目做分析,若作答與晤談 一致性便將錯誤類型及形成錯誤概念的原因歸類,並與九年一貫之能力指標做一 個對照,探討學生是否達到能力指標的學習狀況。30 每一個階段皆邀請專家教授指導研究的程序及方法並不斷收集相關文獻探 討以支持整研究的架構。 研究架構如圖 : 圖 3-1 發展二階段評量工具研究架構圖 二、研究對象 第一步驟研究對象是本研究對象是以研究教師所任課的國一班級二個班級 和任教學校數學教師所任課的三個班級進行施測對象,共有 142 位同學參加。 第二步驟己完成二階段評量工具,施測對象欲擴大為國二學生五個班級,希 望藉此收集到更多或不同的錯誤概念,共有 151 位學生參加。 文獻探討 初步二階段評量工具 發展 開放式測驗 晤談資料 專家效度 第一步驟 樣本施測 診斷施測 學生概念 工具信度 修正二階段評量工具 發展 第二步驟樣本施測 專家效度 完成二階段評量工具 發展